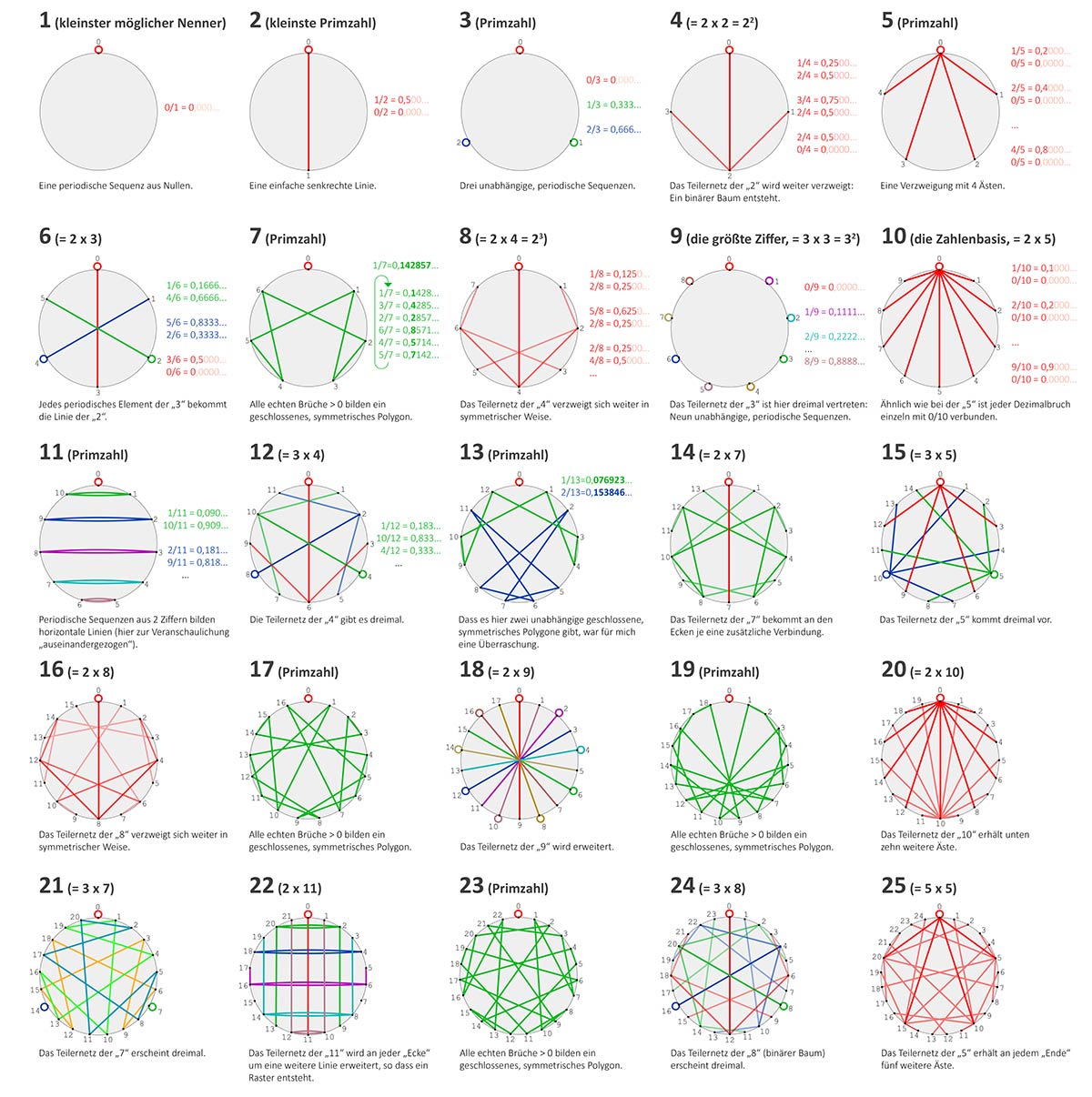
Teilernetze sind (soweit ich weiß) meine eigene Entdeckung.
Echte Brüche 1/z … z‑1/z liegen mit ihrem Wert zwischen 0,0 und 1,0. Mir (und sicherlich Millionen anderer vor mir) ist aufgefallen, dass manche Brüche periodisch sind (z. B. 1/7 = 0,142857..), manche enden nach abzählbarer Anzahl Stellen (z. B. 1/8 = 0,125) und wieder andere haben im Bereich 0/z … z‑1/z alles dabei. Ich wollte das grafisch darstellen und habe dabei diese Muster entdeckt. Vielleicht gibt es das auch schon unter anderem Namen. Ich nenne sie Teilernetze.
Ein Teilernetz verbindet die echten Brüche mit einer Linie, dessen Werte sich um eine Dezimalstelle unterscheiden. Für jede natürliche Zahl ist das dadurch entstehende Netz individuell wie ein Fingerabdruck.
Ich fing mit der Zahl z = 7 an, da sie die periodisch ist und die Sequenz in dezimalen Ziffern nur 6 Stellen lang ist. Dezimal, also Basis b = 10. Ich zeichnete einen Kreis, verteilte darauf 7 Markierungen, die ich oben beginnend mit 0/7 … 6/7 durchnummerierte.

Start ist 1/7, dann wird der Wert mit b=10 multipliziert: 1/7 * 10 = 10/7 und der ganzzahlige Anteil abgezogen: 10/7 — 1 = 3/7. Wir sind auf einem anderen Knoten gelandet und das wird mit einer Linie von 1/7 zu 3/7 gekennzeichnet. Dann gehts mit 3/7 weiter. Also wieder 3/7 * 10 = 30/7, Ganzzahliges abziehen 30/7 — 4 = 2/7. Linie von 3/7 zu 2/7. Weiter… Die entstehende Sequenz ist:
1/7 = 0,142857142857…
3/7 = 0,428571428571…
2/7 = 0,285714285714…
6/7 = 0,857142857142…
4/7 = 0,571428571428…
5/7 = 0,714285714285…
1/7 = 0,142857142857… Die Zähler also zyklisch 1 — 3 — 2 — 6 — 4 — 5 und wieder von vorn.
Das ist das Teilernetz der Zahl 7 zur Basis 10. Am Anfang habe ich das von Hand gezeichnet. Als nächstes wollte ich die 13 ausprobieren. Da erhoffte ich mir eine längere Sequenz mit 12 Schritten. Doch dabei irrte ich mich. Es waren zwei verschachtelte zyklische Sequenzen mit 6 Schritten:
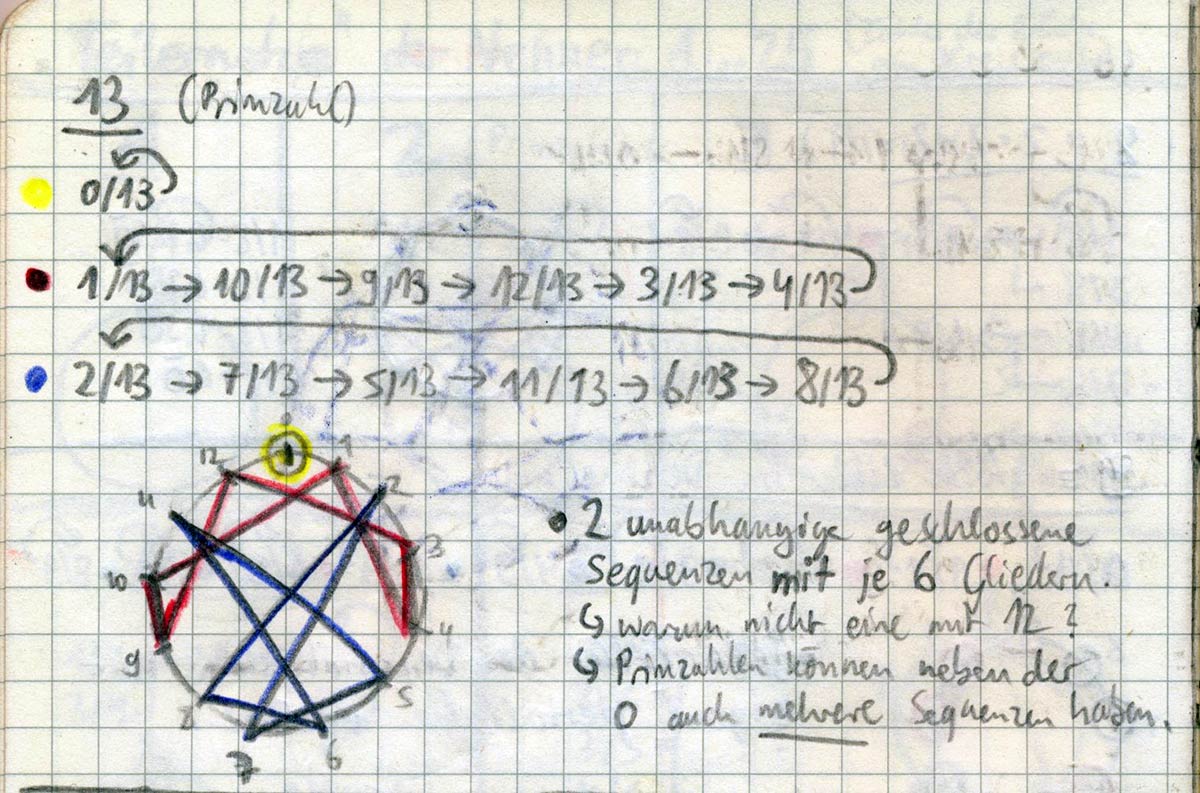
Okay, interessant. Dann probierte ich mal z=19, ob es dann drei Sequenzen gibt. Doch auch hier gab es eine Überraschung:

Das Phänomen dieser Muster mutierte für mich zu einem richtigen Forschungsprojekt. In den Teilernetzen lassen sich nämlich auch die von den echten Teilern (Primfaktoren von z) „geerbten“ Eigenschaften erkennen. Zum Beispiel stecken die Muster von 3 und 5 in der 15. Hier gibt es eine kleine Übersicht:
Zahlen, welche viele 2 und 5 drin haben, beinhalten endliche Brüche, z. B. die 8. Da entstehen Verästelungen, deren Wurzel bei der 0 liegen. Das ist logisch, denn an alle endlichen Brüche wie z. B. 1/8 = 0,125 kann man beliebig viele 0 dran hängen. Nach dem Rechenschema von oben ergibt sich die Sequenz
1/8 = 0,1250; 10 * 1/8 = 10/8; 10/8 — 1 = 2/8
2/8 = 0,250; 10 * 2/8 = 20/8; 20/8 — 2 = 4/8
4/8 = 0,50; 10 * 4/8 = 40/8; 40/8 — 5 = 0/8
0/8 = 0,0; 10 * 0/8 = 0/8 (bleibt so)
endliche Brüche landen irgendwann bei der 0. Und im Teilernetz kann man das gleichzeitig für alle Möglichkeiten sehen!
Als ich bei der Zahl 49 scheiterte, dies von Hand zu zeichnen, schrieb ich Tools, um mir das Zeichnen zu vereinfachen. Dabei verwendete ich PHP zusammen mit POV-Script für farbige und 3D-Darstellungen sowie Javascript/HTML5-Canvas zum Erzeugen von Schwarz-Weiß-Vektorzeichnungen zur Forschung und weiteren Verarbeitung.
Hier zum zum Schluss noch ein komplexeres Beispiel für die Schönheit dieser Graphen. Es ist die Zahl n = 729 = 7*7*7*7 zur Basis b=10. Die 729 Punkte auf dem Kreis werden nach beschriebenen Schema verbunden. Teilernetz T(729;10) sieht so aus:

Edit 18.03.2022
So würde ich die damals von mir entdeckten Muster jetzt mathematisch beschreiben:
- Für jede z ∈ ℕ; z > 1 und Basis b ∈ ℕ; b > 1 gibt es einen Graphen T(z;b), welcher alle Verbindungen zwischen i/z und (i * b mod z)/z enthält.
- T(z;b) beinhaltet die Knoten k[i] = i/z, wobei i ∈ ℕ, 0 < i < z
und deren Verbindungen V(k[i]; k[i * b mod z]), falls i ≠ i * b mod z - T(z;b) ≡ T(z;b+k*z); k ∈ ℕ; k > 1; b>1.
Wenn man zur Basis b die Zahl z addiert, erhält man ein identisches Muster. Das kann man beliebig oft (k-mal) machen. - Jedem Knoten k[i] ein geometrischer Punkt p[i] zugeordnet, welcher auf einer Einheitskreis mit r=1 und M = {x:0;y:0} liegt:
p[i] = { x: cos(i*360/z+ℼ/2), y: ‑sin(i*360/z+ℼ/2) }
p[0] ist dann immer „oben“ bei { x: 0; y: ‑1 }. - Jede Verbindung V(k[i]; k[i * b mod z]) entspricht einer gerichteten Sehne S(p[i];p[i * b mod z]).
a) Wenn in den zur Basis b ausgeschriebenen Wert eines Knotens nach dem Komma eine Ziffer wiederholt, hat er keine Verbindung (Sequenzlänge 1).
b) Die Sehnen bilden geschlossene Polygone, wenn sich in den zur Basis b ausgeschriebenen Werten der beteiligten Knoten nach dem Komma mehr als eine Ziffer wiederholt (Sequenzlänge=Periodenlänge=Anzahl Sehnen).
c) Die Sehnen bilden Verzweigungen mit der Wurzel bei p[0] oder an Punkten von geschlossenen Polygonen, wenn die zur Basis b ausgeschriebenen Werte der beteiligten Knoten nach dem Komma eine endliche Anzahl Ziffern haben. - Spezialfälle:
a) T(z;z) ergibt einen Graphen, wo alle Knoten k[1] … k[z‑1] jeweils mit k[0] verbunden sind. Er enthält somit immer z‑1 Verbindungen.
b) T(z;z+1) ergibt immer einen Graphen ohne Verbindungen.