Endlose Linie mit Ecke
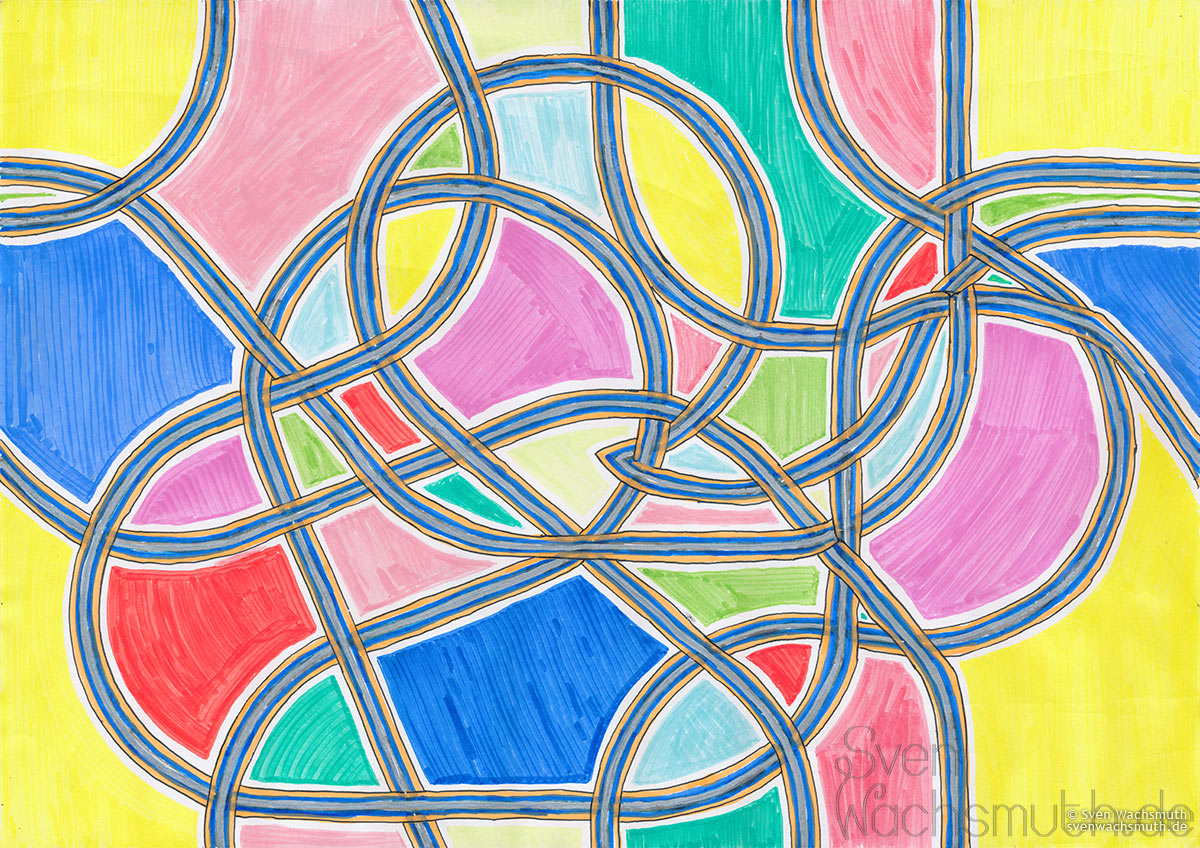
Diese Zeichnung begann ich gestern im Rahmen des Workshops »Kunst nach Plan«. Die letzte Aufgabe bestand darin, sich ein Zeichensystem auszudenken und es selbst umzusetzen.
Begonnen hatte ich in der Mitte, wo jetzt einzige Ecke ihren Eckpunkt hat, mit einem Zirkel ein Kreissegment zu schlagen. Weitere Kreissegmente und gerade Stücke bildeten nach und nach eine Bleistiftlinie, die sich über die Kanten springend fortsetzte. Beim Übergang habe ich genaue Position jeweils zur gegenüberliegenden Kante übertragen und die Richtung ein Stück beibehalten. Der letzte Kreisbogen kam von oben und schloss wieder in einem spitzen Winkel mit dem Anfang und bildet seit dem die Ecke. Dann folgte das mehrfache Nachfahren der Linie mit Acrylstiften. Und schließlich die Füllung der umschlossenen Flächen. Beides unter Berücksichtigung, dass gegenüberliegende Kanten miteinander verbunden sind und nahtlos ineinander übergehen.
Dann habe ich die Vorgehensweise für diese Zeichnung detailliert aufgeschrieben.
Mein Zeichensystem nenne ich »Linien ohne Grenzen«, weil es die Begrenzung der Zeichenfläche aufhebt und diese aktiv für Gestaltungsentscheidungen nutzt. Es entstehen Motive, die in sich zwei Richtungen übergangslos wiederholen.
Hier ist die im Rahmen des Workshops erarbeitete Beschreibung des zugrundeliegenden Zeichensystems:
Mehrere Elemente als Raster
Interessant ist auch, dass sich die Linienführung abhängig von der Anzahl der beteiligten Kachelelemente verändert.
Das Video zeigt den Verlauf der Linie auf der Zeichnung mit den Kantenübergängen. Hier startet und endet der Weg an der Ecke. Es ist eine geschlossene Linie. Zählt man beim Verfolgen des Verlaufs die Kanten, über welche die Linie bei einem Durchlauf die Zeichenfläche verlässt, ergibt sich eine Differenz von 3 Einheiten nach oben und 1 Einheit nach rechts.
In einem ausreichend großen orthogonalen Raster (Bild) endet die Linie genau dort: 3 Elemente nach oben und 1 Element nach rechts. Sie ist plötzlich offen! Dadurch sind mehrere »Linien-Durchläufe« nötig, bis im Raster der Startpunkt wieder erreicht wird. Diese Anzahl scheint wiederum abhängig von der Größe des Rasters und den bereits erwähnten Differenzen bei den Kanten-Übergängen zu sein.
Mathematisch interessant: Wie lang kann so eine Linie in einem Raster werden die bei einem einzelnen Element geschlossen erscheint?