Im Mai 2020 begann ich, „from scratch“ einen Funktionsplotter zu programmieren, welcher den HTML-Canvas als Ausschnitt in der komplexen Zahlenebene betrachtet. Bei der sich draußen ausbreitenden Pandemie war das eine gute Option, mir die Zeit zu vertreiben und dabei noch etwas zu lernen — über Javascript und über komplexe Mathematik. Der Grund war auch, dass ab einer gewissen Komplexität Excel einfach nicht mehr ausreicht, um vernünftige Diagramme zu zeichnen. Vor allem, wenn es genau werden soll und die Zeichnungen später weiterverarbeitet werden sollen.
Die ersten Hürden wie das umrechnen der Bildschirmkoordinaten zu Zeichnungskoordinaten und zurück sowie das Handling bei Änderung der Bildschirmgröße löste ich mit einem Objekt »View«, das zwischen den Koordinatensystemen entsprechend umrechnet und auch ein Raster anzeigen kann.
Punkte werden als Objekte mit Real- und Imaginärteil initialisiert, nicht wie üblich am Bildschirm mit x und y. So kann ich damit auch im komplexen Zahlenbereich rechnen. Es folgten Dreiecke, Kreise und Polygone. Spuren von Punkten aufeinander abrollender Kreise (Zykloiden), Spiegelung am Kreis (Inversion), Überlagerung unterschiedlicher Sinus-Schwingungen (Lissajous) und die Möglichkeit, mit der Maus Punkte zu setzen und auch Punkte entlang anderer Funktionen entlang laufen zu lassen. Mit dem spielerischen Erkunden wuchsen die Javascript-Objekte zu einem nützlichen, rudimentären Framework heran.
Video: Lissajous-Figuren mit nahe beieinender liegenden Frequenzen bilden eine Schwebung, die so aussieht, als würde sich das Teil drehen. Die Bälle erzeuge ich per Mausklick und die laufen dann die ganze Linie entlang.
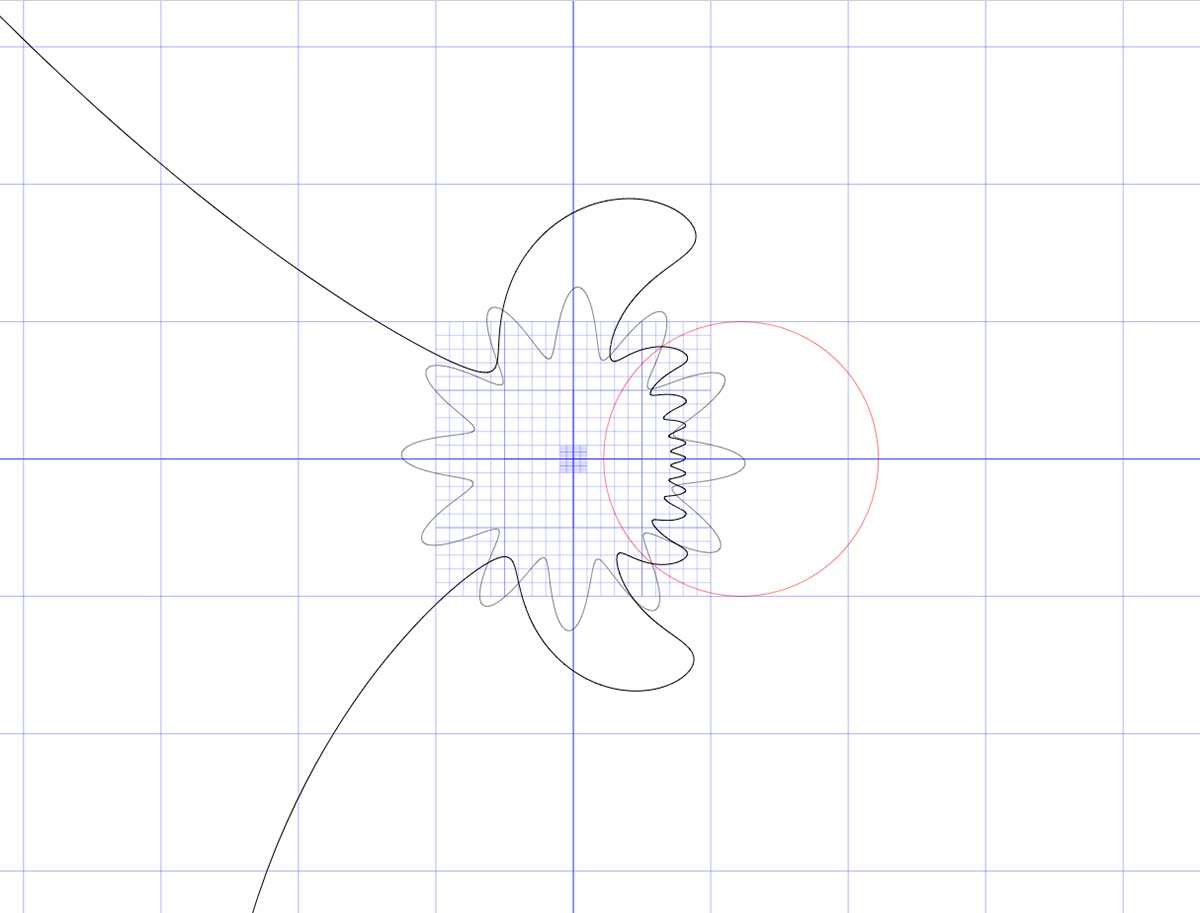
Video: Simulation sogenannter Epizykloiden, aufeinander abrollender Kreise. Auch hier gibt es per Mausklick bunte Bälle entlang der Linie. Und nachfolgend ein Beispiel für die Inversion, d. h. Spiegelung am Kreis: die Zahnradfigur in der Mitte wird am roten Kreis gespiegelt. Auf dem Abbild läuft wieder ein hergeklickter bunter Ball entlang.
Wenn so etwas funktioniert ist es eine richtige Freude, da bunte Bälle entlang zu schicken. (Ja eigentlich habe ich auch andere Hobbies… aber es macht echt Spaß *klick*)
Ich benutze es gern, um mit Javascript mathematische Zeichnungen zu erstellen. Es ist nicht vergleichbar mit den fürs Zeichnen auf dem Canvas etablierten (z. B. p5.js) und erhebt keinen Anspruch auf Vollständigkeit. Vielmehr ist es für mich das Fernglas, um auf meine Art die Welt der komplexen Zahlen zu entdecken. Abgesehen von der notwendigen aber noch weitgehend fehlenden Dokumentation sehe ich erst einmal davon ab, meinen gefühlt unausgereiften Code auf Github zu veröffentlichen.
Aber eins kann ich machen: Dich ermutigen, selbst mit den Möglichkeiten zu beschäftigen, welches das Canvas-Tag bietet. Eine gute und inspirierende Quelle war und ist mir dabei fürs Programmieren The Coding Train und für die Mathematik 3 Blue 1 Brown auf Youtube.