Echte Brüche sind Brüche a/b, wobei a < b ist und der Wert entsprechend kleiner als 1 ist.
Manche davon sind periodisch, andere enden nach einer bestimmten Anzahl Stellen. 2006 ging ich der Sache auf den Grund und entdeckte interessante Strukturen, die ich Teilernetze nannte.
Das ist die Weiterentwicklung meines Teilernetz-Generators von 2016 und läuft auch im Browser. Hier wird PHP für Layout, Erklärungstext und Dateiexport verwendet, Rechnen und Zeichnen mache ich hier nun mit Javascript.
Meine App visualisiert die Struktur der Nachkommastellen von echten Brüchen beliebiger natürlicher Zahlen n (0/n … n‑1/n) und Basen b.
Es werden nur die Werte hinter dem Komma betrachtet, so dass der Wertebereich von 0/n bis n‑1/n auf dem Kreis liegt, so wie die Minuten auf einer Uhr. Jeder Punkt auf dem Kreis entspricht einem Bruch, die Linien zeigen von einem Bruch zu dem, dessen Nachkommastellen um eine Stelle nach links verschoben ist.
Zum Beispiel würden
- 0,125 – 0,25 – 0,5 oder
- 0,142857.. – 0,428561.. – 0,285614.. usw.
miteinander verbunden sein.
Es entstehen Mandala-ähnliche Figuren, die wie ein Fingerabdruck der Zahl zu einer bestimmten Basis einzigartig sind.
Mein Programm berechnet nicht nur alle (!) Nachkommastellen für einen beliebigen echten Bruch, sondern beschreibt auch den Zusammenhang aller echten Brüche einer Zahl n bei einer Basis b.
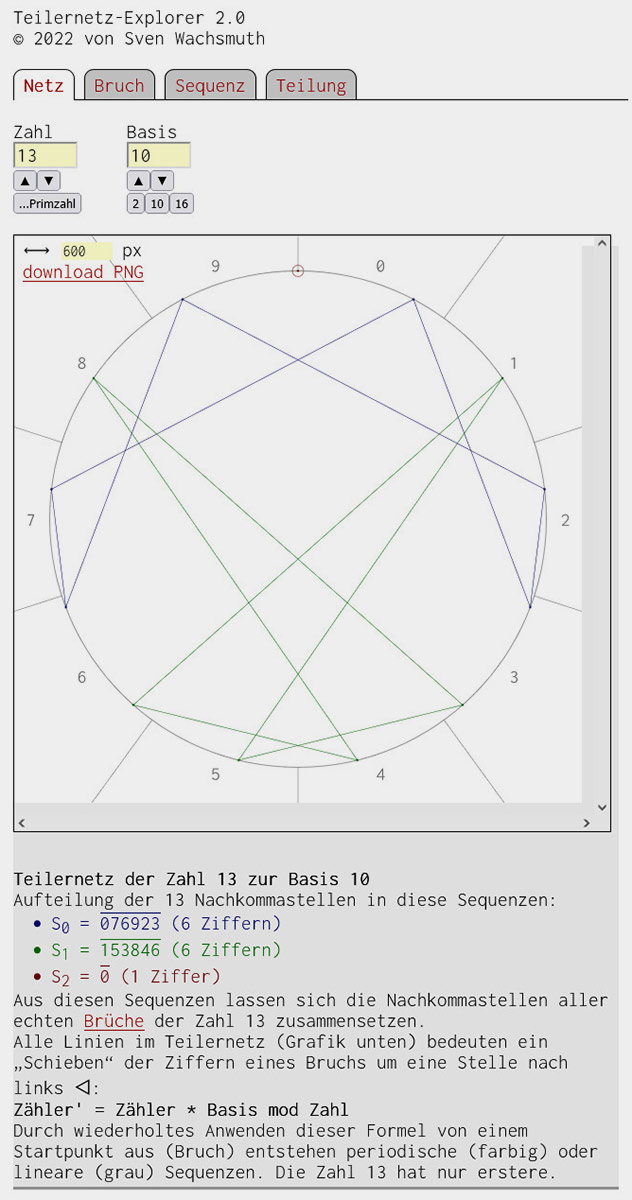
Im Screenshot ist beispielhaft das Teilernetz für die Zahl 13 zur Basis 10 zu sehen. Die 10 Ziffern der Basis bilden Bereiche mit der ersten Nachkommastelle und die 13 Brüche (0/13 … 12/13) Punkte auf dem Kreis. Beides lässt sich oben verändern.
Durch Anklicken der Linien, kann man sich eine Sequenz einzeln betrachten, z. B. die blaue.
Durch Anklicken der Kreislinie kann man sich den Teil des Teilernetzes für einen bestimmten Bruch ansehen, z. B. für 5/13.
Am PC werden Informationen angezeigt, wenn man mit der Maus über die Struktur fährt, beim Smartphone geht das leider nicht.
Unten gibt es automatisch generierte detailierte Infos über das, was man gerade sieht.
Für Basis bis 10 verwende ich die Ziffern 0–9 darüber hinaus verschiedene Alphabete und Symbole und dann verschiedene Arten der Auszeichnung. Das sieht bei Basen >100 ziemlich wild aus.