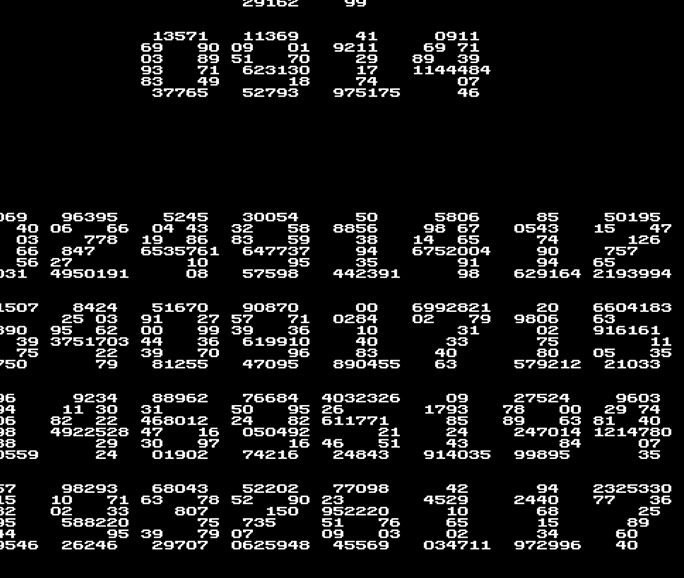
Das ist meine Pi-Tasse. Die erste Stufe besteht aus dem Text »COFFEE AND PI«, dann fängt die Zahl Pi mit den ersten Ziffern »3,14« oben links im ersten Buchstaben »C« an, zieht sich zeilenweise in dieser Größe durch das Motiv und endet bei nach »…6117« bei der 439. Nachkommastelle. Weiter geht’s mit »93105…« innerhalb der »3« oben links los und das zieht sich nun in 0,5 mm großen Ziffern Zeile für Zeile bis unten rechts zur 10.953. Nachkommastelle bzw. endet mit »…99640«.
Es handelt sich hier um den gleichen Algorithmus, den ich 2010 entwickelt habe, um rechnerisch unendlich viele Zeichen auf einer begrenzten Fläche unterzubringen. Die Idee dahinter ist nicht neu: Raster-Zeichen bestehen aus Pixeln, die in der Vergrößerung zu Quadratflächen werden. Diese lassen sich durch Ziffern mit gleicher Größe ersetzen. Dann wird alles wieder vergrößert, so dass Pixel wieder zu Quadratflächen werden. Und so weiter.
Das wiederholte Ersetzen von einfachen Strukturen durch komplexere gibt es z. B. bei einer mathematischen Struktur namens »Cantor-Staub«. Da wird eine Linie in Drittel geteilt und das mittlere Stück rausgenommen. Das wiederholt man immer wieder mit den jeweils verbleibenden Linienstücken. In jedem Schritt verdoppelt sich die Anzahl von Linien, die 1/3 der vorherigen Länge haben. Am Ende sind es unendlich viele unendlich kurze Linien. »Staub« eben.
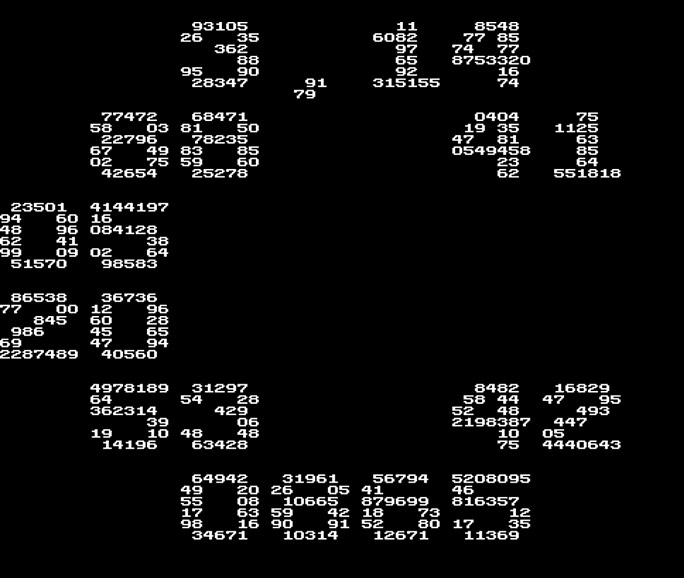
Auf die Tasse passen also die ersten rund 10.000 Stellen der Zahl Pi.
Unten gibt’s noch eine Schippe drauf: Das Tassen-Motiv mit einer weiteren Zahlenebene und damit insgesamt 261.223 Nachkommastellen von Pi!
Das PHP-Script, mit welchem ich das Bild erzeugte, brauchte forderte 5 Gigabyte RAM und brauchte 15 Minuten zum Speichern des rund 24.000 x 9.500 Pixel großen Bildes. Bei 300 dpi Druckauflösung wäre das Bild etwas mehr als 2 Meter breit und die kleinste Ziffern 8x8 Pixel bzw. 0,67 mm hoch.
Anklicken zum Zoomen mit zwei Fingern oder Mausrad:
